本文将探讨当存储介质是外部存储，比如磁盘、闪存时，有哪些主流的存储数据结构(传统的二叉树将不再适用)。 本文以key-value数据库为例讲述不同数据结构的差异。
其KV存储包含以下5个基本操作

  • get(K) 查找key K对应的value
  • put(K,V) 插入键值对（K，V）
  • update(K,V) 查找key K对应的value更新为V
  • delete(K) 删除key K对应的条目
  • scan(K1,K2) 得到从K1到K2的所有key和value

B 系列

B ( B- ) Tree

B树也称B-树,它是一颗多路平衡查找树。我们描述一颗B树时需要指定它的阶数，阶数表示了一个结点最多有多少个孩子结点，一般用字母m表示阶数。当m取2时，就是我们常见的二叉搜索树。

应用的数据库 MongoDB

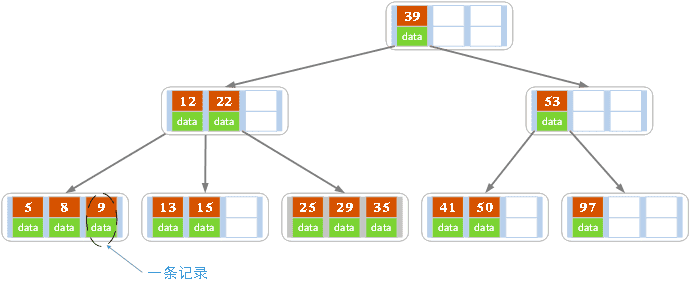
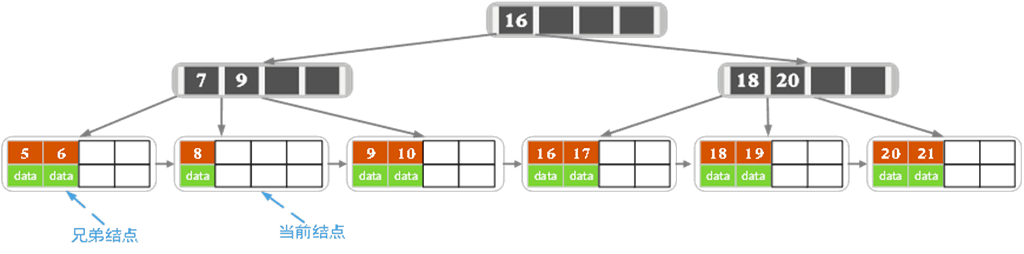
结构图示

以一颗阶数为4的为例，图中数字对应key，data对应value

定义

  1. 每个结点最多有m-1个key。
  2. 根结点最少可以只有1个key。
  3. 非根结点至少有$⌈m/2⌉-1$个key。（最差节点利用率为50%）
  4. 每个结点中的关键字都按照顺序排列，每个关键字的左子树中的所有关键字都小于它，而右子树中的所有关键字都大于它。
  5. 所有叶子结点都位于同一层，或者说根结点到每个叶子结点的长度都相同。
  6. 设某个节点含有n个元素，则
    • 如果是叶子节点，该节点含有n个value
    • 如果是非叶子节点，该节点不仅含有n个value，还存有n+1个子节点的地址（边）

查找

即根据一个key，得到对应的value(data)，也可能找不到。

过程

其步骤如下：

  1. 从根节点开始
  2. 在当前节点内通过二分查找定位到一个最小且>=key的key
  3. 如果key已经命中（相等），则返回该key的值。 如果没有命中，则加载新的子节点，返回第二步继续查找（如果已经是叶子节点，就可以返回不存在）。

复杂度

整个过程时间复杂度是 O(logMlogN),

  • M是阶数， logM对应在节点内做二分查找，每次加载节点都要二分查找一次。
  • N是元素个数， logN对应加载节点的次数，即树的深度

更新

另外更新就是先查找，然后修改value。就不做多的赘述了。不会修改树的结构，但是可能会导致节点地址改动（比如当将一个很小的value替换成一个很大的value，原始节点的物理空间不够，就需要重新将这个节点写入其他地方）。

插入

插入就是查找定位到节点后，在指定位置插入。比较复杂的部分是当节点存在节点满了之后就需要分裂。

最开始插入会先插入到叶子节点。若满则以中值为划分分裂成两个，同时将中值加入到父节点中。如果父节点又满，则进行相同操作。直到分裂向上的节点中没有满。

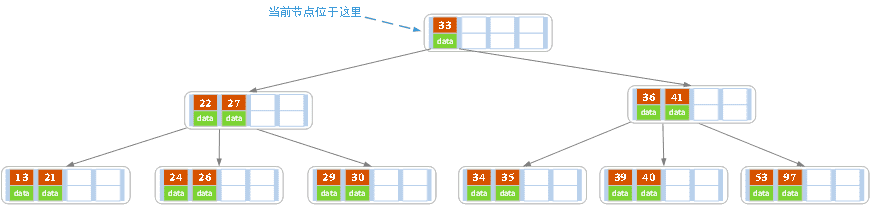
图示

我们以图例来理解这个过程，

  1. 初始： 存在一棵M为5的树,即最大元素个数是4。
  2. 插入成功，但是导致一个叶子节点满
  3. 按中值(27)分裂，并将中值插入到父亲节点
  4. 因为父亲节点满，继续分裂。因为是根节点，所以向上过程直接添加一个新的根节点。整个插入结束。

复杂度

O(logNlogM + M )

  • logNlogM : 访问代价
  • M : 插入造成的移位或者分裂

删除

删除过程相对复杂。 但是其基本原则是，当节点删除一个元素时，
优先从子节点找后继替代自己，如果做不到，就从兄弟节点找（完成一个兄弟到父亲，父亲到自己的转移。若兄弟也做不到，则和兄弟进行合并。（因为此时两个字节点个数都是$⌈m/2⌉-1$）

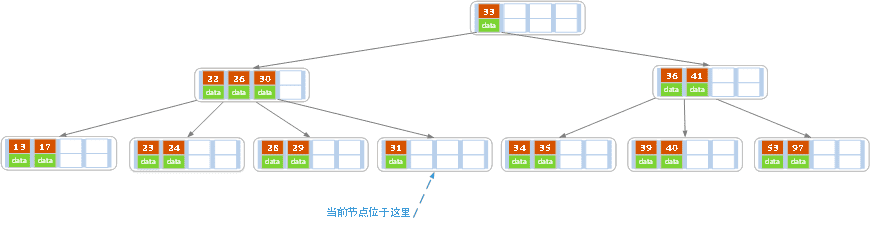
不同情况图示

  1. 初始，阶数为5，即一个节点最少2个元素

  2. 删除21，正常删除，因为删除后节点个数仍然>2

  3. 删除27，在非叶子节点,从子节点替换，

    1. 这里默认优先从右子节点替换 (试探法，减少读取次数，因为大概率情况下不需要转移)
    2. 但是子节点不够，就需要从兄弟节点移动过来。

  4. 删除32

  5. 叶子节点个数不够，但是兄弟节点也无法转移

  6. 合并两个兄弟节点元素和兄弟之间的元素

复杂度

O(logNlogM + M)

  • logNlogM : 访问代价
  • M : 删除造成的移位或者合并

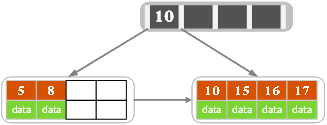
B+ Tree

相比于b树，区别在于

  1. 非叶子节点是索引节点，只存储部分key和子节点地址，不存储value
  2. 所有key和value都会存储在叶子节点中
  3. 叶子节点之间存在顺序指向

查找和更新和B树类似，就不提了。插入和删除思想一致，但是略有差别。

应用的数据库 MySQL 的 innodb

结构图示

插入

插入思想不变。即数据插入到叶子节点，如果满，则分裂，将中值插入到父亲节点，直至某个节点不满。

  1. 如初始
  2. 插入18,叶子满，分裂，中值插入到父亲节点

删除

必须删除叶子节点上的元素，同时更新索引节点上的。由于父亲节点不存在记录，所以都是从从兄弟之间转移。 当无法转移的时候合并节点。

  1. 如初始
  2. 删除7
    1. 删除后发现不足，但是兄弟节点也无法转移
    2. 叶子合并
    3. 索引节点合并

特性

优点

  • 快速查找
  • B+：
    • 对scan(range query，范围扫描 顺序访问)更加友好
    • 索引节点内单个页存储元素个数可以更多，降低树的深度，尤其适合value较大的场景
  • B： 查找更加快（不需要每次访问到子节点）
  • value热更新开销小

缺点

  • 插入操作慢，写
  • 空间放大率高（空间利用率不高）， 数据结构变更容易产生文件空洞
  • 不同节点随机存储在磁盘上，会产生大量的随机IO。

LSM Tree

将日志文件系统与树形数据结构结合适用的形式，提出一种延迟更新、批量写入硬盘的LSM-tree及其算法，

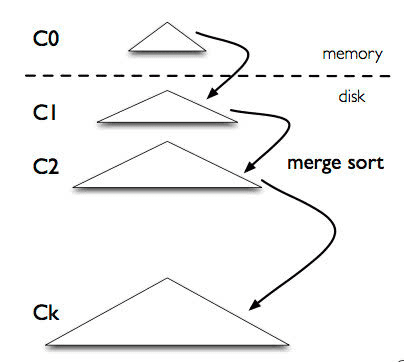
结构

  • C0树（常驻内存）
  • C1-N 树(位于磁盘)

插入、更新、删除

就是将新的键值对放入C0即算插入完成，通过compaction操作去异步维护C0-N之间的关系。

  1. 待C0存储的内容大于一个阈值，就会将内容全部合并到C1中，然后清空C0
  2. 对于C1-N也同理，任何一个Ci查过其阈值后，就讲内容合并到Ci+1

查找

由于compaction导致同一个key可能存在多层中，但是越上层的数据越新。
所以查找则变成从上至下的查询。过程如下

  1. i = 0 (从C0开始)
  2. 如果在Ci中找到了K，则返回value，否则i++然后回到第1步，

特性

优点

  • 大幅度提高插入（修改、删除）性能
  • 空间放大率降低
  • 访问新数据更快，适合时序、实时存储
  • 数据热度分布和level相关

缺点

  • 牺牲了读性能（一次可能访问多个层）
  • 读、写放大率提升

具体实现

LSM Tree对于C树的具体实现很多，理论上Ci树可以是任何允许索引的结构，比如B、hash、二叉树等结构，但是目前业界主流实现可以参考LevelDB和RocksDB。

Bepsilon(ε) Tree / Fractal Tree

一个针对B树做写优化的结构。 可以看做是LSM树和B树的结合

对应系统

被TokuDB 和 the BetrFS 采用。
为了防止歧义，我也将论文中的原文粘贴在引用中。

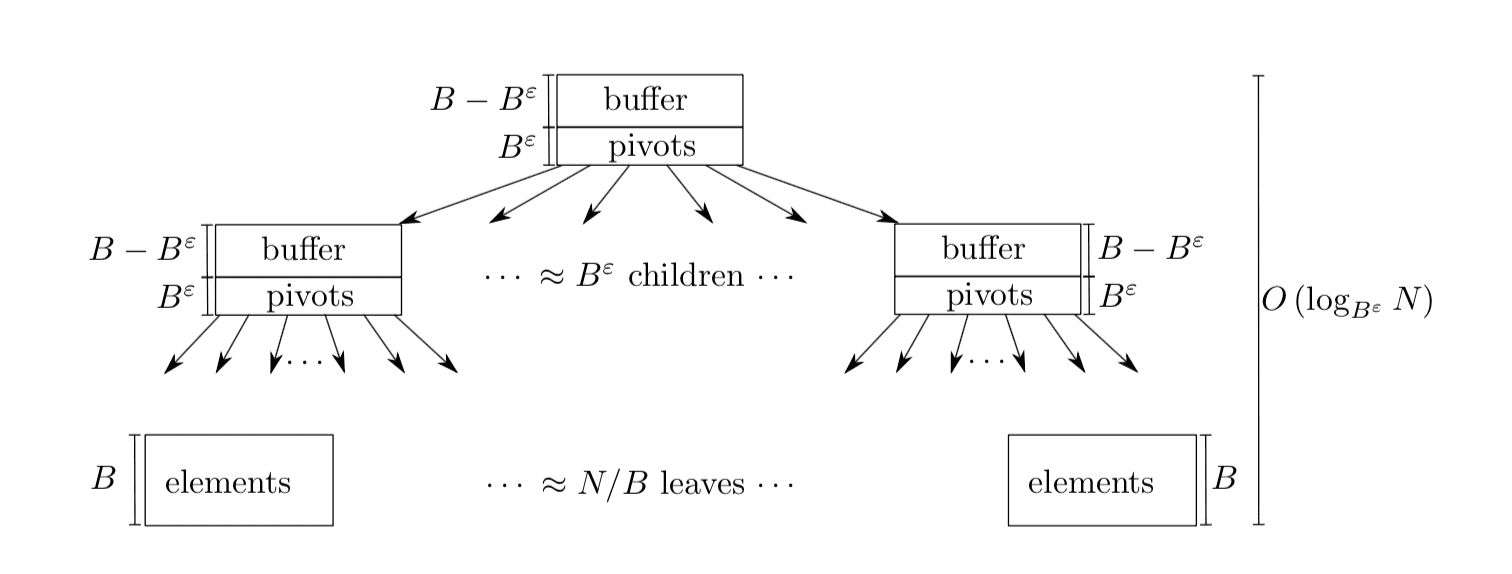
结构

  • 每个node内置一个buffer，这个buffer是持久化存储的。
  • 一个节点的大小为B， 那么存储原始数据的pivots部分大小为Bε和buffer部分大小为B-Bε, ε是0-1之间的一个数

    The distinguishing feature of a Bε-tree is that in- ternal nodes also allocate some space for a buffer, as shown in Figure 1. The buffer in each internal node is used to store messages, which encode updates that will eventually be applied to leaves under this node. This buffer is not an in-memory data structure; it is part of the node and is written to disk, evicted from memory, etc., whenever the node is. The value of ε, which must be between 0 and 1, is a tuning parameter that selects how much space internal nodes use for pivots (≈ Bε) and how much space is used as a buffer (≈ B − Bε).

写操作 （插入和删除）

  1. 每个写操作和删除操作都会编码成message，每个buffer中的message会以二叉搜索树的方式组织（比如红黑树），
  2. 每次都是先写入root node的buffer
  3. 当一个节点的buffer满时，消息将会批量地写给一个子节点
  4. 最终buffer会传递到叶子节点，当叶子节点buffer满时，将改动应用到叶子节点，然后分裂或者合并node的过程就跟B树一样了

Insertions are encoded as “insert messages”, addressed to a particular key, and added to the buffer of the root node of the tree. When enough messages have been added to a node to fill the node’s buffer, a batch of messages are flushed to one of the node’s children. Generally, the child with the most pending messages is selected. Over the course of flushing, each message is ultimately delivered to the appropriate leaf node, and the new key and value are added to the leaf. When a leaf node becomes too full, it splits, just as in a B-tree. Similar to a B-tree, when an interior node gets too many children, it splits and the messages in its buffer are distributed between the two new nodes.

查询

从root到leaf先查询buffer，
buffer中没有再去leafnode里查看。 查询路径和B树相同。

Reference