线段树

适用场景

固定范围内区间统计，统计只能是可以合并的操作如：最值、求和

树状数组

在认识线段树之前，有个熟悉的结构，每一层分布跟归并排序过程类似，就是树状数组，如下：

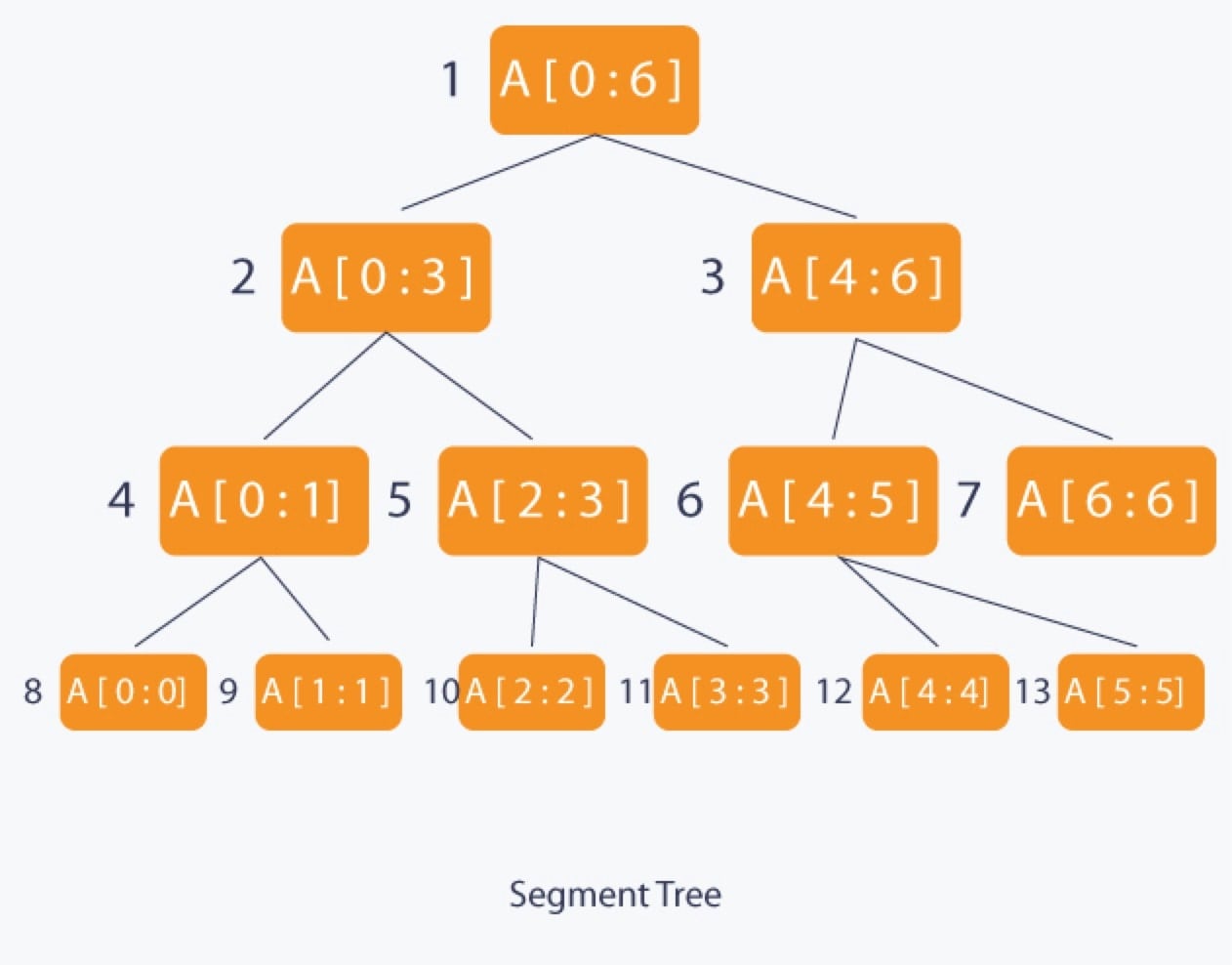
T的根结点代表整个数组所在的区间对应的信息，及arr[0:N]（不含N)所对应的信息。
T的每一个叶结点存储对应于输入数组的每一个单个元素构成的区间arr[i]所对应的信息，此处0≤i<N。
T的每一个中间结点存储对应于输入数组某一区间arr[i:j]对应的信息，此处0≤i<j<N。

其本质思想是分而治之。

代码详解

以如下问题为例来描述样例代码：

我们有一个长度为n的int数组，即A[0..n-1]

需要支持以下几种操作：

找到区间[l..r]内的元素之和
对区间[l..r]内的所有元素都更新为一个新的值x，即a[l..r]=x

理论也可以用链表实现，但是实际效率比如直接用数组实现慢许多。

构建 O(N)

可能有些人会当成N次更新，但是实际可以通过从树状数组尾部遍历来优化

递归版

void build(int node, int start, int end)
{
    if(start == end)
    {
        // Leaf node will have a single element
        tree[node] = A[start];
    }
    else
    {
        int mid = (start + end) / 2;
        // Recurse on the left child
        build(2*node, start, mid);
        // Recurse on the right child
        build(2*node+1, mid+1, end);
        // Internal node will have the sum of both of its children
        tree[node] = tree[2*node] + tree[2*node+1];
    }
}

高效版

// function to build the tree 
void build( int arr[])  
{  
    // insert leaf nodes in tree 
    for (int i=0; i<n; i++)     
        tree[n+i] = arr[i]; 
      
    // build the tree by calculating parents 
    for (int i = n - 1; i > 0; --i)      
        tree[i] = tree[i<<1] + tree[i<<1 | 1];     
}

查找 O(logN)

递归版

int query(int node, int start, int end, int l, int r)
{
    if(r < start or end < l)
    {
        // range represented by a node is completely outside the given range
        return 0;
    }
    if(l <= start and end <= r)
    {
        // range represented by a node is completely inside the given range
        return tree[node];
    }
    // range represented by a node is partially inside and partially outside the given range
    int mid = (start + end) / 2;
    int p1 = query(2*node, start, mid, l, r);
    int p2 = query(2*node+1, mid+1, end, l, r);
    return (p1 + p2);
}

高效版

// function to get sum on interval [l, r) 
int query(int l, int r)  
{  
    int res = 0; 
    // loop to find the sum in the range 
    for (l += n, r += n; l < r; l >>= 1, r >>= 1) 
    { 
        if (l&1)  
            res += tree[l++]; 
        if (r&1)  
            res += tree[--r]; 
    } 
    return res; 
}

更新 O(logN)

递归版

void update(int node, int start, int end, int idx, int val)
{
    if(start == end)
    {
        // Leaf node
        A[idx] += val;
        tree[node] += val;
    }
    else
    {
        int mid = (start + end) / 2;
        if(start <= idx and idx <= mid)
        {
            // If idx is in the left child, recurse on the left child
            update(2*node, start, mid, idx, val);
        }
        else
        {
            // if idx is in the right child, recurse on the right child
            update(2*node+1, mid+1, end, idx, val);
        }
        // Internal node will have the sum of both of its children
        tree[node] = tree[2*node] + tree[2*node+1];
    }
}

高效版
如果是更新一个区间，那么就必须使用类似上面的递归分治过程。
如果是只更新一个元素，那可以用如下方法。

// function to update a tree node 
void updateTreeNode(int p, int value)  
{  
    // set value at position p 
    tree[p+n] = value; 
    p = p+n; 
      
    // move upward and update parents 
    for (int i=p; i > 1; i >>= 1) 
        tree[i>>1] = tree[i] + tree[i^1]; 
}

二维线段树

即矩阵（假设N行M列）下的线段树，应对矩形区间内的更新和查询，有三种实现方法

基础的方法：每一行当成一个一维线段树，那么更新和查询复杂度变成O(NlogM)
四分树：即每次递归向下时分成四份更新和查询复杂度变成(logM * logN)
分段线段树：本质同四分树，时间复杂度也相同。但是代码相对简单些。每次递归向下也是二分，只是对行二分和对列二分间隔进行（类似KD树），比如深度为偶数时对行二分，深度为奇数时对列二分。